要想利用整除性解决问题，首先要求考生对整除的性质有比较到位的把握，落实到公务员考试中，具体就是能够熟练判断任意给出的一个数能否被2~9所整除。判断方法如下：

    被2整除：所有的偶数。

    被3整除：所有数位上的数字之和能被3整除。如123456各个数位上数字之和为21能被3整除，那么123456就能被3整除。

    被4整除：后两位能够被4整除。因为100能被4整除，也就是说百位之前不管是任何数字都一定能被4整除，只需要判断后两位。如123456的后两位是56能被4整除，那么123456就能被4整除。

    被5整除：末位数字是0或者5。

    被6整除：同时满足能被2整除和能被3整除的条件，即能被3整除的偶数就能被6整除。如123456也能被6整除。

    被8整除：后三位能够被8整除。因为1000能被8整除，也就是说千位之前不管是任何数字都一定能被8整除，只需要判断后三位。如123456的后三位456恰好能被8整除，所以123456也能被8整除。

    被9整除：所有数位上的数字之和能被9整除。如123456各个数位上数字之和为21不能被9整除，所以123456也就不能被9整除。

    细心的考生可能会发现，我们在这里没有总结能被7整除的判断方法。首先可以很明确的回答，被7整除的规律是有的，但同时更明确的告诉大家，在公务员考试中绝对不会考到这个规律，因为它太复杂了。被7整除的判断规律只适用于大于1000的数，将百位以上的数字与后三位数字做差，如果这个差值能被7整除，那么这个数就能被7整除。这一规律在公务员考试中并不具备实用价值，考生不需要掌握。而如果在考试中出现了需要判断某个数能否被7整除的情况，考生也无需慌张，直接做一个简单的一位数除法就可以了。

    公务员考试中最不够用的是时间，也正因此我们不但要保证准确率，更要注重提升做题的速度，以便在有限的时间内可以完成更多的题目。在很多数学运算的题目中，只需要利用整除性进行简单的判断，就可以规避常规解法繁琐的计算过程，快速而准确的选出正确的答案。

    【例题1】：2002年国家公务员考试B类20题

    一个正方形被分成了五个大小相等的长方形。每个长方形的周长都是36米，问这个正方形的周长是（     ）

    A.56米             B.60米              C.64米              D.68米

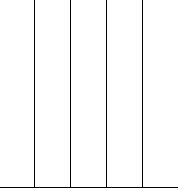
    【答案】：B

    【新东方名师贾柱保解析】：如果采用常规解法，设正方形的边长为L，则五个长方形的周长之和等于大正方形的周长再加上中间被重复计算两次的四条边，即

    9L＝36×5

    通过解方程可以求得每条边的长度L＝15米，周长为60米。

    但本题利用整除性几乎不用计算，因为一条边可以被五等分，因此大正方形的边长一定是5的倍数，周长也一定可以被5整除，只有B选项符合。新东方北斗星贾柱保老师提醒各位考生，在公务员考试中不必担心小长方形的宽会出现非整数情况，根据历年命题的规律，此类题目中所有的数字一定都是整数。

    【例题2】：2003年国家公务员考试A类9题

    某剧场共有100个座位，如果当票价为10元时，票能售完，当票价超过10元时，每升高2元，就会少卖出5张票。那么当总的售票收入为1360元时，票价为多少（    ）

    A.12元             B.14元              C.16元              D.18元

    【答案】：C

    【新东方名师贾柱保解析】：本题若按常规解法，可设票价相对于10元升高了2n元，则最终卖出的票的张数为100－5n，根据题意可以得到方程

    （10＋2n）×（100－5n）＝1360

    这是一个一元二次方程，求解比较麻烦，需要考生先把方程整理为一般形式，再利用二次方程的求根公式进行求解，计算量非常大。

    若利用整除性，则本题可以非常快速解决。因为无论最终票价为多少，票价和卖出票的张数都一定是整数，并且总售票收入等于票价与卖出张数的乘积，因此总收入一定能被票价所整除。首先排除A、D，因为12和18中都含有因子3，而1360不能被3整除，自然也不能被12或18整除。经过简单判断，1360恰好能被16整除，而14不能整除1360，因此票价只能为16元。与通过列方程解出的答案一致。

    【例题】3：2005年国家公务员考试二卷44题

    小红把平时生下来的全部五分硬币先围成一个正三角形，正好用完，后来又改围成一个正方形，也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币，则小红所有五分硬币的总价值是（    ）

    A.1元              B.2元               C.3元               D.4元

    【答案】：C

    【新东方名师贾柱保解析】：本题实际是几何问题中的一种，即阵列问题。如果设总的硬币数量为N，则可以列出方程

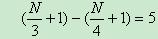
    需要注意围成三角形和正方形时每条边上的硬币数量应该是总数的1/3或1/4再多一枚。虽然在本题中并不影响最终的结果，但考生对此类问题一定要有明确的把握。

    但其实本题并不需要考虑这种关系，因为既然全部硬币能够围成一个正三角形，那说明硬币的总数一定能被3整除，总的钱数也就一定能被3整除，只有C选项符合条件。

    【例题4】：2009年国家公务员考试109题

    已知甲、乙两人共有260本书，其中甲的书有13%是专业书，乙的书有12.5%是专业书，问甲有多少本非专业书（    ）

    A.67                B.75                C.87                 D.174

    【答案】：C

    【新东方名师贾柱保解析】：本题看似条件不足，无法通过列方程的方法进行求解，但实际上只需要把握住隐含条件就可以迎刃而解。因为书只能以整本的形式出现，也就是说甲的全部书籍数量乘以13%一定是整数，那么甲的全部书籍数量只能是100本或者200本，同时还需要满足乙的全部书籍数量乘以12.5%也是整数。简单进行试验之后，可发现甲共有100本书，乙共有160本书，则甲的非专业书占100本的87%，有87本。

    【例题5】：2006年北京市社会在职人员考试11题

    37×18＋27×42的值是（    ）

    A.1800              B.1850              C.1900              D.2000

    【答案】：A

    【新东方名师贾柱保解析】：本题在计算上不存在任何的困难，所考查的只是考生的计算速度，因为本题绝对不会出现“不会算”的问题。在新东方北斗星贾柱保老师接触过的学生中，计算速度最快的也花费了超过30秒的时间才能算出1800。单纯对于本题来讲，超过3秒钟就已经不值了，原因很简单，请看：18和27都能被9整除，因此最后的计算结果也一定能被9整除，只有A选项1800符合。

    【例题6】：2009年湖南省公务员考试117题

    请计算99999×22222＋33333×33334的值（    ）

    A.3333400000        B.3333300000        C.3333200000        D.3333100000

    【答案】：B

    【新东方名师贾柱保解析】：本题与例题5比较类似，虽然在考场上并不会有人真正按部就班去进行五位数的乘法运算，但多数考生可能会采用常规做法，以“拆分法”求解。通过观察发现原式的前后两个部分中可以拆出相同因子，因此可将原式变形为

    33333×3×22222＋33333×33334＝33333×（66666＋33334）＝3333300000

    这是数学运算的基本方法与技巧之一，考生应该对此有比较熟练的掌握。但若能够进一步观察发现，99999和33333是都可以被3整除的，那么只要在选项中选择出只能被3整除的B项就可以了。

    【例题7】：2008年陕西省公务员考试57题

    火树银花楼7层，层层红灯按倍增，共有红灯381，试问四层几个红灯？（    ）

    A.24                B.28                 C.36               D.37

    【答案】：A

    【新东方名师贾柱保解析】：由题意可知，每层的红灯数构成了一个公比为2的等比数列，如果设首项为 ，则由等比数列的求和公式可以得到方程

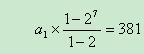
    通过解方程可以求出 ，再结合公比推出第四层的红灯数。这是本题的常规解法，但我们可以明显发现，这种解法对考生的数学能力要求较高，考生要知道等比数列的求和公式，而且计算量也较大，很费时间。

    实际上本题给出的红灯总数是一个“幌子”，完全可以不用。既然每层红灯的数量是按倍增加的，那么第四层的红灯数一定是第一层红灯数的8倍，也就是说第四层红灯的数量一定能被8整除，只有A选项符合这一条件。

    通过以上的一些例题，简要的为各位考生展示了整除性在公务员考试中的若干应用。能够利用乘除性解决的问题当然远远不止这几道，这里只不过为考生们选取了比较有代表性的一些典型题目，冰山一角。通过这些题目，希望能够帮助大家打开思路，在解题中能够试图寻找新的途径和方法。当我们在面对一道“难题”而屡攻不破的时候，换一个思考的方向，也许就会“山穷水复疑无路，柳暗花明又一村”。