要解决国家公务员考试中数学部分的题目，我们曾经说过需要掌握三大武器，即六种基本运算、方程、数图结合。这其中，基本运算和方程两大武器通过综合运用，可以应付多半的题目种类，但要解决某些较复杂的题目则显得有些力不从心。这时候就需要动用到第三种武器了，也就是通过题目与图形的结合来降低难度，理清解题思路。在公务员考试中常见的数图结合题目，大致可以分为以下几种：

    一、行程问题

    并非所有的行程问题都需要用到数图结合的方法。通常情况下，利用 是解决行程问题的有效途径。这里我们特指那些考查两个或以上物体的运动，并且条件比较复杂，单纯利用 的关系式不太容易求解的一部分行程问题。具体说来，这类问题通常需要用到所谓的比值等量关系式来求解，即

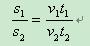
    在解决这类问题的时候，首先画出路程图，大大有助于分析各物体的运动状态。

    【例题1】：2000年国家公务员考试35题

    甲、乙两人从400米的环形跑道的一点A背向同时出发，8分钟后两人第三次相遇。已知甲每秒钟比乙每秒钟多行0.1米，那么，两人第三次相遇的地点与A点沿跑道上的最短距离是（    ）

    A.166米            B.176米             C.224米             D.234米

    【答案】：B

    【新东方名师贾柱保解析】：假设甲沿跑道顺时针方向行走，乙沿逆时针方向行走，首先画出两人运动的路程图如下：

    其中A点为出发点，B点为第一次相遇点，C点为第二次相遇点，D点为第三次相遇点。由A点到B点，甲乙两人走的路程总和恰好是一个圆周。由B点到C点，甲乙两人走的路程总和也是一个圆周，由C到D同理。也就是说，从A点出发经过三次相遇后，甲乙两人走过的总路程恰好是三倍的跑道长，1200米。而甲比乙多走0.1×60×8＝48米，所以甲总共走的路程是 米。因此D点A点沿跑道上的最短距离是176米。

    【例题2】：2005年湖南省公务员考试43题

    甲从A地步行到B地，出发1小时40分钟后，乙骑自行车也从同地出发，骑了10公里时追到甲。于是，甲改骑乙的自行车前进，共经5小时到达B地，这恰是甲步行全程所需时间的一半。问骑自行车的速度是多少公里/小时？（    ）

    A.12                B.10                C.16                D.15

    【答案】：A

    【新东方名师贾柱保解析】：本题甲乙二人的行进过程比较复杂，单纯通过题干的叙述很难弄清整个运动过程，因此我们先根据题目的叙述画出由A到B的路程图。

    图中C点表示甲步行1小时40分所到达的位置，D点表示乙骑自行车追上甲时的位置，AD的长度是10公里。由于需要求的只是自行车的速度，因此我们先不考虑甲、乙两个人各自怎么走，而考虑自行车和人这两个物体各自怎么运动。由题意可知，自行车从A点出发以后便始终没有停，走完了一个全程，所用的时间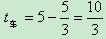小时。而人步行走完全程需要的时间 小时，所以我们可以得到自行车和人步行的速度关系为

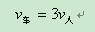
    接下来考查乙骑车追甲的过程，这是行程问题的基本类型之一，追及问题。则根据题意可以列出方程

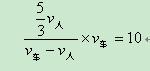
    代入车与人的速度关系比值，可求得自行车的速度为12公里/小时。

    总体而言，对于行程问题，画出正确的路程图，是找准题目中各个数量之间关系的前提，也是降低题目难度的有效手段。

    二、集合问题

    数图结合应用最典型的一类题目，要数集合问题。在这类问题中，图形对于解题的帮助功能被发挥得淋漓尽致。对于集合问题而言，解决的方法总结到两个字，就是“画圈”。如果用比较规范的语言来叙述，就是应用文氏图的方法来解题。根据具体题目的不同，又可以分为“一个圈”和“三个圈”两种类型。新东方北斗星贾柱保老师提醒各位考生，近年来集合问题在公务员考试中频繁出现，针对这类问题的解决方法，考生应该有比较系统的掌握。

    【例题3】：2004年国家公务员考试A类46题

    某大学某班学生总数为32人，在第一次考试中有26人及格，在第二次考试中有24人及格，若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（    ）

    A.22                B.18                C.28                D.26

    【答案】：A

    【新东方名师贾柱保解析】：本题是标准的集合问题，也是比较简单的类型，只需要画“一个圈”就可以解决。根据题意，将全班学生分为如下四种：

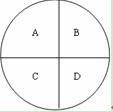
    整个圆表示全部学生总数，A部分表示两次考试都及格的人数，B部分表示第一次考试及格而第二次考试不及格的人数，C部分表示第一次考试不及格而第二次考试及格的人数，D部分表示两次考试都不及格的人数。则根据题意可得

    A＋B＋C＋D＝32

    A＋B＝26

    A＋C＝24

    D＝4

    解方程组可求得A＝22，即两次考试都及格的人数是22人。

    【例题4】：2007年国家公务员考试55题

    一名外国游客到北京旅游。他要么上午出去游玩，下午在旅馆休息；要么上午休息，下午出去游玩，而下雨天他只能一天都呆在屋里。期间，不下雨的天数是12天。他上午呆在旅馆的天数为8天，下午呆在旅馆的天数为12天。他在北京共呆了（    ）

    A.16天             B.20天              C.22天              D.24天

    【答案】：A

    【新东方名师贾柱保解析】：本题也仅用“一个圈”就可以解决，但是需要对文氏图进行简单的变形。

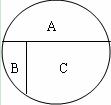
    依然用整个圆表示此人在北京呆的总天数，A部分表示上午出去、下午休息的天数，B部分表示下午出去、上午休息的天数，C部分表示上下午都不出去的天数，则由题意可得

    A＋B＝12

    B＋C＝8

    A＋C＝12

    三式相加再除以2，得到A＋B＋C＝16，即此人在北京呆的总天数为16天。

    【例题5】：2005年国家公务员考试二卷45题

    外语学校有英语、法语、日语教师共27人，其中只能教英语的有8人，只能教日语的有6人，能教英、日语的有5人，能教法、日语的有3人，能教英、法语的有4人，三种都能教的有2人，则只能教法语的有（    ）

    A.4人              B.5人               C.6人               D.7人

    【答案】：B

    【新东方名师贾柱保解析】：本题对全部教师的分类比较多，单靠画“一个圈”难以解决，因此我们采用画“三个圈”的方法，将全部教师分成如下所示的部分：

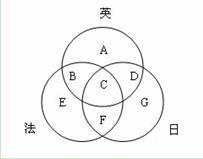
    由题意可得：A＋B＋C＋D＋E＋F＋G＝27，A＝8，G＝6，C＋D＝5，C＋F＝3，B＋C＝4，C＝2，可求得只能教法语的人数为E＝5人。

    【例题6】：2006年国家公务员考试二卷43题

    某工作组有12名外国人，其中6人会说英语，5人会说法语，5人会说西班牙语；有3然既会说英语又会说法语，有2人既会说法语又会说西班牙语，有2人既会说西班牙语又会说英语；有1人这三种语言都会说。则只会说一种语言的人比一种语言都不会说的人多（    ）

    A.1人              B.2人               C.3人               D.4人

    【答案】：C

    【新东方名师贾柱保解析】：本题与例题5类似，也是采用“三个圈”的文氏图来解决。

    根据题意，可得方程组

    A＋B＋C＋D＋E＋F＋G＝12

    A＋B＋C＋D＝6

    B＋C＋E＋F＝5

    C＋D＋F＋G＝5

    B＋C＝3

    C＋F＝2

    C＋D＝2

    C＝1

    对上述各式进行整理，可得A＋E＋G－C＝3，即只会说一种语言的人比一种语言都不会说的人多3人。

    对于集合问题，其解题思路和方法比较固定，考生只要能掌握文氏图的解法，面对此类型的题目只需要照搬应用就可以了。

    三、其它问题

    除却前述两大类问题之外，在公务员考试中还存在若干其它类型的问题需要用到数图结合的方法，但这些题目往往零星分布在不同类型的题目之中。

    【例题7】：2005年国家公务员考试一卷49题

    甲对乙说：当我的岁数是你现在岁数时，你才4岁。乙对甲说：当我的岁数到你现在岁数时，你将有67岁。甲乙现在各有（    ）

    A.45岁，26岁       B.46岁，25岁       C.47岁，24岁       D.48岁，23岁

    【答案】：B

    【新东方名师贾柱保解析】：根据题意我们画出如下的示意图：

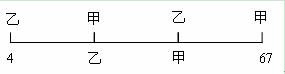
    由图中我们可以发现，从4岁到67岁之间恰好被等分成了三段，每一段都是甲、乙两人的年龄差（因为任意两个人之间的年龄差永远不变），所以甲比乙大
 

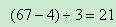    岁

    则乙的年龄是4＋21＝25岁，甲的年龄是25＋21＝46岁，正确答案为B项。也可以直接在四个选项中选出甲、乙年龄差是21岁的选项，只有B。

    【例题8】：2006年国家公务员考试二卷37题

    在一条公路上每隔100公里有一个仓库，共有5个仓库，一号仓库存有10吨货物，二号仓库存有20吨货物，五号仓库存有40吨货物，其余两个仓库都是空的。现在要把所有的货物集中存放在一个仓库里，如果每吨货物运输1公里需要0.5元运输费，则最少需要运费（    ）

    A.4500元           B.5000元            C.5500元            D.6000元

    【答案】：B

    【新东方名师贾柱保解析】：要计算最少的总运费，关键是要确定把全部的货物集中到哪一个仓库里。根据题意，最初的货物分布情况是：

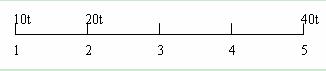
    首先我们确定，不可能把全部货物都集中到1号仓库，因为那样一来最重的40吨货物走的距离最远，运费肯定不能够最省。那么不管要放到2、3、4、5号仓库中的哪一个，1号仓库的10吨货物一定要搬，并且必然会经过2号仓库。此时货物的分布情况变成了：

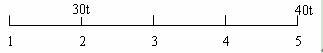
    此时这两份货物不管放到哪一个仓库，所要经过的总路程数是固定的300公里。那么为了使总的运费最少，必须要满足最重的40吨运输距离最短，最短距离为0公里，即全部货物都集中到5号仓库，此时运费最省，总运费为

    （10×100＋30×300）×0.5＝5000元

    以上通过一部分题目为大家展示了数图结合方法在公务员考试数量关系部分的一些应用，希望各位考生能够通过总结、归纳和一定的练习，掌握数图结合这一重要方法，真正攻破从题目的叙述中感觉无从下手的那一部分难题，在公务员考试备考之路上再下一城。